Kodowanie
Komputer jest urządzeniem służącym do przetwarzania informacji. Informacją są liczby, a także inne obiekty, takie jak litery, wartości logiczne i tym podobne. Ponieważ komputer jest urządzeniem zbudowanym z układów cyfrowych, każda informacja prze­twarzana przez niego musi być reprezentowana przy pomocy dwóch stanów - wysokiego i niskiego. Duża część tej informacji to liczby, stąd przyjęło się nazywać te stany jedynką i zerem (l i 0). Możemy zatem stwierdzić, że wszelka informacja w komputerze musi wy­stępować w postaci zerojedynkowej czyli binarnej. Potrzebne są też reguły przekształcania różnych postaci informacji na informację binarną. Proces przekształcania informacji jednego rodzaju postaci na inną postać nazywamy kodowaniem.

Kodowaniem nazywamy przyporządkowanie poszczególnym obiektom zbioru ko­dowanego odpowiadających im elementów zwanych słowami kodowymi, przy czym każdemu słowu kodowemu musi odpowiadać dokładnie jeden element kodowany.
Zbiorem kodowanym może być zbiór dowolnych obiektów, przykładowo liter, symboli graficznych czy np. stanów logicznych. Proces kodowania poglądowo przed­stawiony jest na rysunku 1.1.

Rysunek 1.1. Graficzna interpretacja procesu kodowania

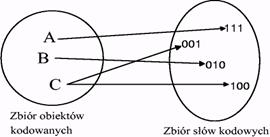
Zgodnie z rysunkiem litera A będzie reprezentowana przez słowo kodowe (w skrócie kod) 111, litera B przez 010 zaś litera C przez 001 lub 100. Fakt, że literze C odpowiadają dwa słowa kodowe, nie przeszkadza w poprawnym przetwarzaniu informacji, aczkolwiek stanowi pewne utrudnienie procesu kodowania. Sytuacja od­wrotna, gdy jedno słowo kodowe odpowiadałoby dwóm literom (na przykład A - 001 i B - 001), byłaby niedopuszczalna. Jeżeli w procesie przetwarzania informacji otrzy­malibyśmy kod 001, nie bylibyśmy w stanie określić przy dekodowaniu, czy w wyni­ku odpowiada on literze A, czy B.
Jak wspomnieliśmy, informacja kodowana w komputerze jest bardzo różnorod­na. Mogą to być teksty (czyli ciągi znaków), polecenia do wykonania przez komputer (na przykład instrukcje dla procesora), wartości logiczne czy też liczby. W ostatnim przypadku będziemy mówić o tak zwanych kodach liczbowych. Będą to kody przed­stawiające liczby, z reguły dziesiętne, w postaci binarnej. Poniżej podajemy definicję kodu liczbowego oraz kilka przykładów najczęściej używanych kodów.

Kodem liczbowym nazywamy taki kod, który liczbom dowolnego systemu bę­dzie przyporządkowywał słowa kodowe w postaci zerojedynkowej.

Przykład Naturalny kod binarny (NKB) Jeżeli dowolnej liczbie dziesiętnej przyporządkujemy odpowiadającą jej liczbę binarną, to otrzymamy naturalny kod binarny (NKB).

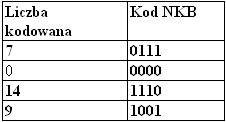
Kilka przykładowych wartości liczb kodowanych i odpowiadających im stów kodowych (przy założeniu długości słów kodowych równej 4) zawiera tabela l .2.

Tabela 1.2. Przykłady słów kodu NKB

Kod prosty BCD
Sposób konstruowania słowa kodowego w kodzie prostym BCD jest następujący: 1. Każdej cyfrze dziesiętnej przyporządkowujemy czterocyfrową liczbę dwójkową (zwaną tetradą) w kodzie NKB (gdybyśmy zamiast słów kodu NKB użyli innego kodu, np. kodu Gray'a, wówczas otrzymalibyśmy kod BCD Gray'a). Przypo­rządkowanie to przedstawione jest w tabeli 1.3.

Tabela 1.3. Przyporządkowanie cyfr dziesiętnych tetradom NKB

Do góry