Systemy liczbowe Działanie układów cyfrowych oparte jest na wykorzystaniu dwóch stanów elek­trycznych tych układów, zwanych stanem niskim (ang. Iow - L) i stanem wysokim (ang. high - H). Przy ich użyciu musimy przedstawić wszystkie rodzaje informacji występujące w układach cyfrowych. W tym celu stosowane są określone struktury, takie jak dwójkowy (binarny) system liczbowy oraz kody, umożliwiające reprezenta­cję informacji w układach cyfrowych.

System dwójkowy Ludzie w sposób naturalny przyzwyczajeni są do liczenia w systemie dziesięt­nym, dlatego też konstrukcję i użycie systemu dwójkowego przedstawiamy przez analogię do systemu dziesiętnego.
Do zapisu dowolnej liczby bez znaku system dziesiętny wykorzystuje dziesięć symboli graficznych, zwanymi cyframi: 0, l, 2, 3, 4, 5, 6, 7, 8, 9. Przy ich użyciu je­steśmy w stanie przedstawić dowolną liczbę. System dziesiętny, podobnie jak i system dwójkowy jest systemem pozycyjnym. Liczbę 425D (D oznacza zapis liczby w syste­mie dziesiętnym) możemy przedstawić jako następującą sumę:

Widzimy więc, że cyfra na danej pozycji mnożona jest przez odpowiednią potęgę liczby 10, przy czym wykładnik tej potęgi zależy od położenia (pozycji) danej cyfry w liczbie. Uwaga! Pozycje cyfr w liczbie numerujemy od 0 (najmłodsza cyfra). Po­szczególne mnożniki, zwane inaczej wagami, w systemie dziesiętnym noszą nazwę odpowiednio: jedynek (10°=1), dziesiątek (101=10), setek (102=100) i tak dalej. Poszczególne wagi w systemie dziesiętnym są potęgami liczby 10, dlatego jest ona zwana podstawą tego systemu (p = 10). Podsumowując, formalny zapis an-1......a0 w systemie dziesiętnym oznacza:

gdzie:
  i - jest numerem pozycji w liczbie,
  ai - oznacza dowolną z cyfr od 0 do 9,
  n - jest ilością cyfr (pozycji) w liczbie.
Ponieważ w systemie dziesiętnym dysponowaliśmy dziesięcioma cyframi dla za­pisania dowolnej liczby bez znaku, w systemie dwójkowym musimy do tego celu używać jedynie dwóch cyfr: 0 i 1. Jak już wspomnieliśmy, obydwa systemy są syste­mami pozycyjnymi, co oznacza, że cyfrę na danej pozycji mnoży się przez określoną wagę. Dla systemu dwójkowego podstawą jest liczba 2 (p = 2) i wagami są odpo­wiednie potęgi tej liczby. Kolejne pozycje liczby zwane są więc pozycjami jedynek, dwójek, czwórek, ósemek i tak dalej. Zapis w systemie dwójkowym, zwanym inaczej systemem binarnym, liczby 10100B (litera B sygnalizuje liczbę w systemie dwójko­wym) oznacza:
10100B = 1*24+0*23 + l*22 + 0*2i + 0*20 = l* 16+ 0*8 + 1*4 + 0*2 + 0*1 = 16+ 4 = 20D Uogólniając, zapis an-1......a0B w systemie dwójkowym będzie oznaczał:

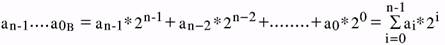
Wzór ten, określający sposób zapisu liczby w systemie dwójkowym, pozwala jednocześnie na dokonanie konwersji (przeliczenia) liczby zapisanej w systemie dwój­kowym na liczbę zapisaną w systemie dziesiętnym. Jedną z metod konwersji liczby dziesiętnej na dwójkową pokażemy na przykła­dzie, pomijając uzasadnienie jej poprawności. Metoda ta polega na wykonywaniu kolejnych dzieleń całkowitych, z zapisem reszty, przez liczbę 2. Rozpoczynamy od podzielenia liczby przeliczanej przez 2. Kolejne dzielenie wykonujemy na liczbie będącej ilorazem poprzedniego dzielenia. Postępowanie kontynuujemy aż do mo­mentu otrzymania jako wyniku 0. Reszty dzieleń ustawione w odpowiedniej kolejno­ści dają poszukiwaną liczbę binarną.

Przykład
Dokonać konwersji liczby 23D na liczbę binarną.
Rozwiązanie

A zatem 23D = 10111B

System heksadecymalny
System heksadecymalny, czyli szesnastkowy, nie jest używany bezpośrednio przez układy cyfrowe, jest natomiast wygodnym, zwartym sposobem zapisu liczb binarnych. Stosowany jest on często przez programistów czy też przy wyświetlaniu informacji cyfrowej na ekranie (na przykład w programach typu debugger).
W systemie heksadecymalnym do zapisu dowolnej liczby dysponujemy szesna­stoma cyframi. Ponieważ symboli graficznych oznaczających liczby arabskie jest dziesięć, brakuje symboli sześciu cyfr. Przyjęto więc, że będą one oznaczane począt­kowymi literami alfabetu (dużymi lub małymi). Zatem A oznacza dziesiątkę, B jede­nastkę, aż do cyfry F, która oznacza piętnastkę. Pełny zestaw cyfr heksadecymalnych jest więc następujący:
ai    {0, l, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}
gdzie ai oznacza cyfrę heksadecymalną. Liczba szesnaście jest podstawą tego systemu. Formalny zapis an-1....a0H oznacza więc:

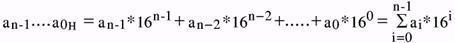
gdzie ai jest dowolną cyfrą heksadecymalną.

Przykład
ZnaleŸć liczbę dziesiętną odpowiadającą liczbie heksadecymalnej 4C2H.
Rozwiązanie
Zgodnie z podanym wzorem oraz wcześniejszymi informacjami:
4C2H = 4 * 162+ C * 161 + 2 * 16° = 4 * 256 + 12 * 16 + 2 * l = 1218D
Konwersji liczby dziesiętnej na heksadecymalną można dokonać metodą analo­giczną do pokazanej dla systemu dwójkowego, wykonując kolejne dzielenia z resztą przez liczbę 16. Należy jednak pamiętać, że reszty z dzielenia zapisujemy w postaci cyfr heksadecymalnych, czyli np. resztę 14 zapisujemy jako E.

Przykład
Dokonać konwersji liczby 2123D na liczbę hekadecymalną.
Rozwiązanie
2123 : 16 = 132    r=B
132 : 16 = 8    r=4
8 : 16 = 0    r=8
A zatem 2123D=B48H

Najistotniejsza cechą systemu heksadecymalnego jest łatwość przechodzenia od zapisu binarnego do heksadecymalnego i na odwrót, przez co zapis heksadecymalny staje się zwartym zapisem liczb binarnych. Zobaczymy to na przykładzie.

Przykład
Zapisać liczbę binarną 1001011010B w postaci liczby heksadecymalnej.
Rozwiązanie
Przy przejściu od liczby binarnej do heksadecymalnej wykorzystujemy fakt, że każdej cyfrze heksadecymalnej odpowiada określona kombinacja czterech cyfr binar­nych i na odwrót. Pokazuje to tabela 1.1.
Przeliczaną liczbę binarną dzielimy od końca (czyli od najmłodszej pozycji) na czwórki, a następnie każdą z nich zapisujemy w postaci jednej cyfry heksadecymalnej, zgodnie z tabelą 1.1. Jeżeli ostatni fragment liczby nie jest pełną czwórką, możemy ją dopełnić do czwórki zerami. Tak więc dla liczby binarnej 001001011010: 0010 || 0101 || 1010B = 25AH
Podobnie możemy postąpić przy przeliczaniu w drugą stronę. Wówczas każdą cyfrę heksadecymalną zapisujemy w postaci czwórki cyfr binarnych. Ewentualne nieznaczące zera na początku liczby binarnej można w wyniku pominąć.

Tabela 1.1. Cyfry heksadecymalne i odpowiadające im liczby binarne

Przykład
Zapisać liczbę heksadecymalną 7cd5H w postaci liczby binarnej.
Rozwiązanie
7CD5H= 0111 l 1100 l 1101 l 0101B = 111110011010101B Proszę porównać długości liczb heksadecymalnych i odpowiadających im liczb dwójkowych. Wyjaśni to wygodę stosowania zapisu heksadecymalnego.

Do góry